분할 정복 알고리즘 정리

한 문제를 작은 문제로 나누어 해결하는 문제 유형을 분할 알고리즘, 각 문제들을 다시 합쳐 정답을 구하는 문제를 정복 알고리즘이라고 부른다.

• DP와 다른 점
  • 다이나믹 프로그래밍은 분할한 작은 문제들이 서로에게 영향을 미침 => 중복
    • 이전 문제를 기록해 다음 문제 해결(memorization)
  • 분할 문제는 일반적으로 부분이 중복되지 않아 한 문제씩 해결해 풀이 가능

분할 정복 알고리즘

• 합병 정렬
• 퀵 정렬
• 큰 수 곱셈 (카라추바 알고리즘)
• FFT

1. 이분 탐색

정렬되어 있는 리스트에서 특정 값을 빠르게 찾는 알고리즘이다. 이분 탐색 알고리즘은 $O(log N)$의 시간이 걸린다.

정렬이 되어 있지 않은 리스트에서 어떤 값을 탐색하려면 리스트에 있는 값들을 모두 살펴봐야 하므로 복잡도가 $O(N)$이 된다.

$N \to \frac{N}{2} \to \frac{N}{4} \to \frac{N}{8} \to 1$ => N을 절반으로 나누어 1을 만들었을 때의 횟수: $log N$

whlie(left <= right)		// list의 left와 right 사이에 원소 find 존재
{                               // left > right라면 해당 리스트에 find 원소 없음 => 반복문 종료
    mid = (left + right) / 2;	// mid 위치 갱신
    
    if(list[mid] == find)       // list에서 find원소를 찾았을 경우
    {
        position = mid;
        break;                  // 반복문 종료
    }
    else if(list[mid] > find)   // find가 mid보다 작은 경우
        right = mid - 1;	// right를 mid의 한 칸 왼쪽으로 이동
    else                        // find가 mid보다 큰 경우
        left = mid + 1;		// left를 mid의 한 칸 오른쪽으로 이동
}

2. 합병 정렬

원소를 절반씩 나누어 각각 정렬한 후, 정렬 결과를 하나로 합치는 알고리즘이다.

리스트의 원소 개수가 1이 될 때까지 나누어야 이후 순서대로 정렬할 수 있으므로, 원소를 모두 분할하는데 $O(logN)$ 만큼의 시간이 걸린다.

리스트를 나누고 나면, 각 배열은 정렬되어 있으므로 각 배열의 원소 크기들을 비교해가며 새 배열으로 병합한다.

합병 순서는 다음과 같다.

1. 나누어진 두 개의 배열을 합친 길이의 임시 배열 생성
2. 두 배열의 데이터를 하나씩 비교해 더 작은 값을 임시 배열에 적재
3. 두 배열 중 하나를 모두 순회할 때까지 3과정 반복
4. 남아 있는 배열의 나머지 원소들은 정렬되어 있으므로 그대로 임시 배열으로 복사

원소를 순회해 리스트를 한 번 합치는데 필요한 시간복잡도는 $O(N)$이므로, 배열을 모두 정렬하는데 걸리는 시간은 $O(N log N)$ 이 된다.

void sort(int start, int end)		// start번째부터 end번째까지 정렬하는 함수
{
    if (start == end) return;		// 수의 개수가 1개면 더이상 정렬할 수 없으므로 리턴해준다.

    int mid = (strart + end) / 2;
    
    sort(start, mid);			// 왼쪽 부분 정렬
    sort(mid + 1, end);			// 오른쪽 부분 정렬
    merge(start, end);			// 왼쪽과 오른쪽이 모두 정렬되어 있으므로 합병 수행
}

void merge(int start, int end)
{
    // mid를 기준으로 나눈 배열들의 각 첫 번째 원소 left, right
    // 임시 배열 인덱스 index (원소 덮어씌우기 방지용 배열)
    int mid = (start + end) / 2;
    int left = start, right = mid + 1; 
    int index = 0;			
    
    while(left <= mid && right <= end) //left는 mid까지, right는 end까지 순회
    {
        // left와 right 비교 후 더 작은 수 tmp에 적재
	if(list[left] <= list[right]) tmp[index++] = list[left++];
        else tmp[index++] = list[right++];
    }
    
    // 한 쪽에 남아있는 원소가 있을 경우 tmp에 그대로 적재
    while(left <= mid) tmp[index++] = list[left++];
    while(right <= end) tmp[index++] = list[right++];
    
    // 임시 배열 원소를 다시 list로 복사
    for(int i = start; i <= end; i++)
        list[i] = tmp[i - start];
}

3. 퀵 정렬

배열에서 원소를 골라 피벗으로 지정한 후 피벗을 기준으로 크거나 같은 값은 모두 오른쪽으로, 작은 값은 모두 왼쪽으로 옮기는 알고리즘이다.

피벗의 위치는 고정되고 나뉘어진 부분 리스트들이 순환 호출으로 피벗의 앞과 뒤에서 다시 퀵 정렬을 수행한다.

리스트에서 피벗을 특정하므로 한번 순환호출이 진행될 때마다 하나의 원소는 반드시 위치가 정해진다.

=> 정렬 알고리즘이 무조건 끝난다는 것을 보장한다.

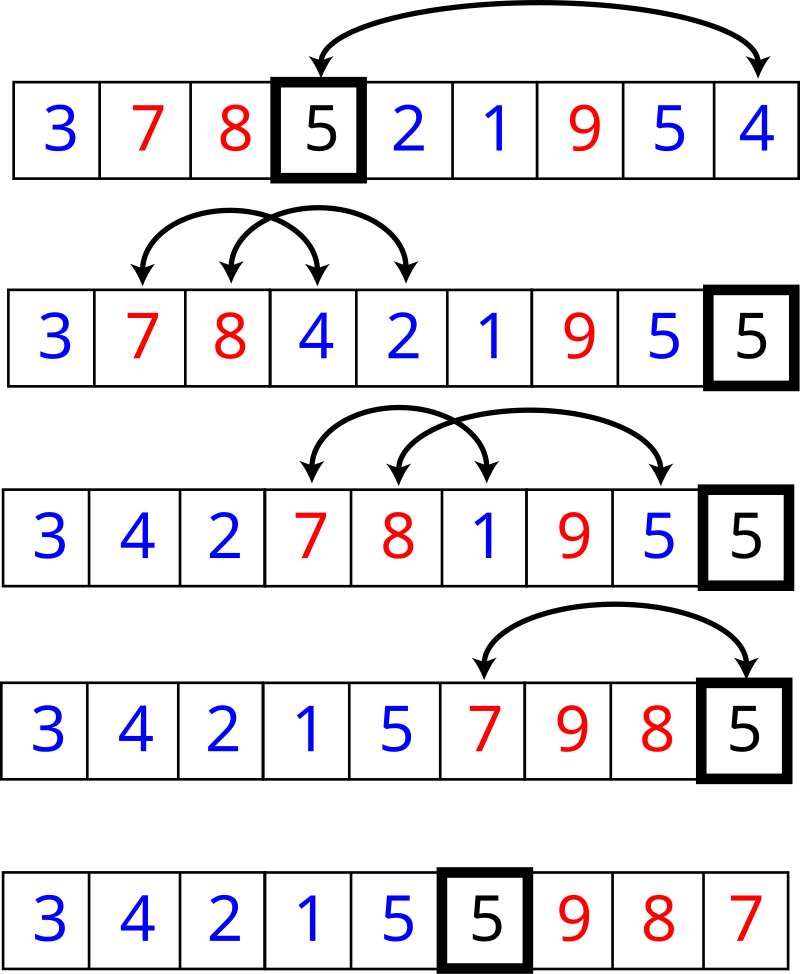
그림 출처: [위키백과] 퀵 정렬

1. 피벗으로 선정된 5를 리스트 마지막 위치로 이동
2. 배열 순회용 변수를 두 개 만들어(index, left) 배열의 첫 번째 원소부터 마지막 원소까지 순회
   1. index 위치의 데이터가 피벗보다 작다면 index 원소와 left 원소를 교환한 후 left 위치 한 칸 이동
   2. index 위치의 데이터가 피벗보다 크다면 아무 동작도 하지 않음
   3. 비교가 하나 끝날 때마다 index 위치 한 칸씩 이동
3. 순회가 모두 끝났다면 left를 기준으로 왼쪽은 모두 피벗보다 작은 값이므로 left 원소와 피벗 원소의 위치 교환

랜덤 피벗으로 인해 합병 정렬과 다르게 리스트를 비균등하게 분할하는 특징이 있으며,

평균적인 상황에서 매우 빠른 속도로 동작한다.

단, 불균형 분할의 특성 상 최악의 경우에는 시간 복잡도가 $O(N^{2})$까지 걸린다는 단점이 있다.

개선된 피벗 선택

최악의 경우를 방지하기 위해 리스트의 처음, 중간, 마지막 부분의 중위법을 이용해 분할한다. 해당 분할 방법을 사용하면 리스트가 균형적으로 분할될 가능성이 높아지므로 안정성이 개선된다.

퀵 정렬의 시간복잡도

• 최선: $O(N log N)$
• 평균: $O(N log N)$
• 최악: $O(N^{2})$
• 별도의 데이터 이동과 리스트 분할 과정이 없으므로 같은 시간 복잡도인 다른 정렬 알고리즘에 비해 속도가 준수함

4. 퀵 셀렉트

정렬되지 않은 리스트에서 k번째 작은 수를 찾는 알고리즘이다.

퀵 소트와 다르게 한 방향 리스트만 출력해 최적의 경우 시간 복잡도가 $O(N)$으로 줄어든다.

단 최악의 경우 시간 복잡도가 $O(N^{2})$까지 늘어날 수 있으므로, 리스트를 모두 정렬한 이후 k번째 인덱스를 찾는 것이 일반적이다.

=> 안정적으로 시간복잡도 $O(N log N)$ 유지